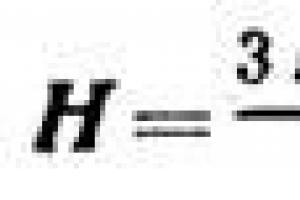Законы де Моргана – это логические правила, установленные шотландским математиком Огастесом де Морганом, связывающие пары логических операций при помощи логического отрицания.

Огастес де Морган заметил, что в классической логике справедливы следующие соотношения:

not (А and В) = (not А) or (not В)

not (А or В) = (not А) and (not В)

В более привычной для нас форме данные соотношения можно записать в следующем виде:

Законы де Моргана можно сформулировать следующим образом:

I закон де Моргана: Отрицание дизъюнкции двух простых высказываний равносильно конъюнкции отрицаний этих высказываний.

II закон де Моргана: Отрицание конъюнкции двух простых высказываний равносильно дизъюнкции отрицаний этих высказываний.

Рассмотрим применение законов де Моргана на конкретных примерах.

Пример 1. Преобразовать формулу так, чтобы не было отрицаний сложных высказываний.

Воспользуемся первым законом де Моргана, получим:

к отрицанию конъюнкции простых высказываний В и С применим второй закон де Моргана, получим:

таким образом:

В итоге мы получили равносильное высказывание, в котором нет отрицаний составных высказываний, а все отрицания относятся только к простым высказываниям.

Проверить справедливость решения можно с помощью таблиц истинности. Для этого составим таблицы истинности для исходного высказывания:

и для высказывания, полученного в результате преобразований, выполненных с помощью законов де Моргана:

Таблица 1.

			В/\С	А\/В/\С

Как видим из таблиц, исходное логическое высказывание и логическое высказывание, полученное с помощью законов де Моргана – равносильны. Об этом говорит тот факт, что в таблицах истинности мы получили одинаковые наборы значений.

В главе 8 рассматривались такие виды объектов нечисловой природы, как нечеткие и случайные множества. Цель настоящего приложения - глубже изучить свойства нечетких множеств и показать, что теория нечетких множеств в определенном смысле сводится к теории случайных множеств. Для достижения поставленной цели формулируется и доказывается цепь теорем.

В дальнейшем считается, что все рассматриваемые нечеткие множества являются подмножествами одного и того же множества Y .

П2-1. Законы де Моргана для нечетких множеств

Как известно, законами же Моргана называются следующие тождества алгебры множеств

Теорема 1. Для нечетких множеств справедливы тождества

(3)

Доказательство теоремы 1 состоит в непосредственной проверке справедливости соотношений (2) и (3) путем вычисления значений функций принадлежности участвующих в этих соотношениях нечетких множеств на основе определений, данных в главе 8.

Тождества (2) и (3) назовем законами де Моргана для нечетких множеств . В отличие от классического случая соотношений (1), они состоят из четырех тождеств, одна пара которых относится к операциям объединения и пересечения, а вторая - к операциям произведения и суммы. Как и соотношение (1) в алгебре множеств, законы де Моргана в алгебре нечетких множеств позволяют преобразовывать выражения и формулы, в состав которых входят операции отрицания.

П2-2. Дистрибутивный закон для нечетких множеств

Некоторые свойства операций над множествами не выполнены для нечетких множеств. Так, за исключением случая, когда А - "четкое" множество (т.е. функция принадлежности принимает только значения 0 и 1).

Верен ли дистрибутивный закон для нечетких множеств? В литературе иногда расплывчато утверждается, что "не всегда". Внесем полную ясность.

Теорема 2. Для любых нечетких множеств А, В и С

В то же время равенство

справедливо тогда и только тогда, когда при всех

Доказательство . Фиксируем произвольный элемент . Для сокращения записи обозначим Для доказательства тождества (4) необходимо показать, что

Рассмотрим различные упорядочения трех чисел a, b, c. Пусть сначала Тогда левая часть соотношения (6) есть а правая т.е. равенство (6) справедливо.

Пусть Тогда в соотношении (6) слева стоит а справа т.е. соотношение (6) опять является равенством.

Если то в соотношении (6) слева стоит а справа т.е. обе части снова совпадают.

Три остальные упорядочения чисел a, b, c разбирать нет необходимости, поскольку в соотношение (6) числа b и c входят симметрично. Тождество (4) доказано.

Второе утверждение теоремы 2 вытекает из того, что в соответствии с определениями операций над нечеткими множествами (см. главу 8)

Эти два выражения совпадают тогда и только тогда, когда, когда что и требовалось доказать.

Определение 1. Носителем нечеткого множества А называется совокупность всех точек , для которых

Следствие теоремы 2. Если носители нечетких множеств В и С совпадают с У, то равенство (5) имеет место тогда и только тогда, когда А - "четкое" (т.е. обычное, классическое, не нечеткое) множество.

Доказательство. По условию при всех . Тогда из теоремы 2 следует, что т.е. или , что и означает, что А - четкое множество.

П2-3. Нечеткие множества как проекции случайных множеств

С самого начала появления современной теории нечеткости в 1960-е годы началось обсуждение ее взаимоотношений с теорией вероятностей. Дело в том, что функция принадлежности нечеткого множества напоминает распределение вероятностей. Отличие только в том, что сумма вероятностей по всем возможным значениям случайной величины (или интеграл, если множество возможных значений несчетно) всегда равна 1, а сумма S значений функции принадлежности (в непрерывном случае - интеграл от функции принадлежности) может быть любым неотрицательным числом. Возникает искушение пронормировать функцию принадлежности, т.е. разделить все ее значения на S (при S 0), чтобы свести ее к распределению вероятностей (или к плотности вероятности). Однако специалисты по нечеткости справедливо возражают против такого "примитивного" сведения", поскольку оно проводится отдельно для каждой размытости (нечеткого множества), и определения обычных операций над нечеткими множествами с ним согласовать нельзя. Последнее утверждение означает следующее. Пусть указанным образом преобразованы функции принадлежности нечетких множеств А и В . Как при этом преобразуются функции принадлежности ? Установить это невозможно в принципе. Последнее утверждение становится совершенно ясным после рассмотрения нескольких примеров пар нечетких множеств с одними и теми же суммами значений функций принадлежности, но различными результатами теоретико-множественных операций над ними, причем и суммы значений соответствующих функций принадлежности для этих результатов теоретико-множественных операций, например, для пересечений множеств, также различны.

В работах по нечетким множествам довольно часто утверждается, что теория нечеткости является самостоятельным разделом прикладной математики и не имеет отношения к теории вероятностей (см., например, обзор литературы в монографиях ). Авторы, сравнивавшие теорию нечеткости и теорию вероятностей, обычно подчеркивали различие между этими областями теоретических и прикладных исследований. Обычно сравнивают аксиоматику и сравнивают области приложений. Надо сразу отметить, что аргументы при втором типе сравнений не имеют доказательной силы, поскольку по поводу границ применимости даже такой давно выделившейся научной области, как вероятностно-статистические методы, имеются различные мнения. Напомним, что итог рассуждений одного из наиболее известных французских математиков Анри Лебега по поводу границ применимости арифметики таков: "Арифметика применима тогда, когда она применима" (см. его монографию ).

При сравнении различных аксиоматик теории нечеткости и теории вероятностей нетрудно увидеть, что списки аксиом различаются. Из этого, однако, отнюдь не следует, что между указанными теориями нельзя установить связь, типа известного сведения евклидовой геометрии на плоскости к арифметике (точнее к теории числовой системы - см., например, монографию ). Напомним, что эти две аксиоматики - евклидовой геометрии и арифметики - на первый взгляд весьма сильно различаются.

Можно понять желание энтузиастов нового направления подчеркнуть принципиальную новизну своего научного аппарата. Однако не менее важно установить связи нового подхода с ранее известными.

Как оказалось, теория нечетких множеств тесно связана с теорией случайных множеств. Еще в 1974 г. в работе было показано, что нечеткие множества естественно рассматривать как "проекции" случайных множеств. Рассмотрим этот метод сведения теории нечетких множеств к теории случайных множеств.

Определение 2. Пусть - случайное подмножество конечного множества У. Нечеткое множество В, определенное на У, называется проекцией А и обозначается Proj A, если

(7)

при всех

Очевидно, каждому случайному множеству А можно поставить в соответствие с помощью формулы (7) нечеткое множество В = Proj A. Оказывается, верно и обратное.

Теорема 3. Для любого нечеткого подмножества В конечного множества У существует случайное подмножество А множества У такое, что В = Proj A.

Доказательство. Достаточно задать распределение случайного множества А . Пусть У 1 - носитель В (см. определение 1 выше). Без ограничения общности можно считать, что при некотором m и элементы У 1 занумерованы в таком порядке, что

Введем множества

Для всех остальных подмножеств Х множества У положим Р(А=Х)=0 . Поскольку элемент y t входит во множества Y(1), Y(2),…, Y(t) и не входит во множества Y(t+1),…, Y(m), то из приведенных выше формул следует, что Если то, очевидно, Теорема 3 доказана.

Распределение случайного множества с независимыми элементами, как следует из рассмотрений главы 8, полностью определяется его проекцией. Для конечного случайного множества общего вида это не так. Для уточнения сказанного понадобится следующая теорема.

Теорема 4. Для случайного подмножества А множества У из конечного числа элементов наборы чисел и выражаются один через другой.

Доказательство. Второй набор выражается через первый следующим образом:

Элементы первого набора выразить через второй можно с помощью формулы включений и исключений из формальной логики, в соответствии с которой

В этой формуле в первой сумме у пробегает все элементы множества Y\X, во второй сумме переменные суммирования у 1 и у 2 не совпадают и также пробегают это множество, и т.д. Ссылка на формулу включений и исключений завершает доказательство теоремы 4.

В соответствии с теоремой 4 случайное множество А можно характеризовать не только распределением, но и набором чисел В этом наборе а других связей типа равенств нет. В этот набор входят числа следовательно, фиксация проекции случайного множества эквивалентна фиксации k = Card(Y) параметров из (2 k -1) параметров, задающих распределение случайного множества А в общем случае.

Будет полезна следующая теорема.

Теорема 5 . Если Proj A = B , то

Для доказательства достаточно воспользоваться тождеством из теории случайных множеств формулой для вероятности накрытия из главы 8, определением отрицания нечеткого множества и тем, что сумма всех P(A=X) равна 1.

П2-4. Пересечения и произведения нечетких и случайных множеств

Выясним, как операции над случайными множествами соотносятся с операциями над их проекциями. В силу законов де Моргана (теорема 1) и теоремы 5 достаточно рассмотреть операцию пересечения случайных множеств.

Теорема 6. Если случайные подмножества А 1 и А 2 конечного множества У независимы, то нечеткое множество является произведением нечетких множеств Proj A 1 и Proj A 2 .

Доказательство. Надо показать, что для любого

По формуле для вероятности накрытия точки случайным множеством (глава 8)

Как известно, распределение пересечения случайных множеств можно выразить через их совместное распределение следующим образом:

Из соотношений (9) и (10) следует, что вероятность накрытия для пересечения случайных множеств можно представить в виде двойной суммы

Заметим теперь, что правую часть формулы (11) можно переписать следующим образом:

(12)

Действительно, формула (11) отличается от формулы (12) лишь тем, что в ней сгруппированы члены, в которых пересечение переменных суммирования принимает постоянное значение. Воспользовавшись определением независимости случайных множеств и правилом перемножения сумм, получаем, что из (11) и (12) вытекает равенство

Для завершения доказательства теоремы 6 достаточно еще раз сослаться на формулу для вероятности накрытия точки случайным множеством (глава 8).

Определение 3. Носителем случайного множества С называется совокупность всех тех элементов для которых

Теорема 7. Равенство

верно тогда и только тогда, когда пересечение носителей случайных множеств и пусто.

Доказательство. Необходимо выяснить условия, при которых

Тогда равенство (13) сводится к условию

Ясно, что соотношение (14) выполнено тогда и только тогда, когда р 2 р 3 =0 при всех т.е. не существует ни одного элемента такого, что одновременно и , а это эквивалентно пустоте пересечения носителей случайных множеств и . Теорема 7 доказана.

П2-5. Сведение последовательности операций над нечеткими множествами

к последовательности операций над случайными множествами

Выше получены некоторые связи между нечеткими и случайными множествами. Стоит отметить, что изучение этих связей в работе (эта работа выполнена в 1974 г. и доложена на семинаре "Многомерный статистический анализ и вероятностное моделирование реальных процессов" 18 декабря 1974 г. - см. ) началось с введения случайных множеств с целью развития и обобщения аппарата нечетких множеств Л. Заде. Дело в том, что математический аппарат нечетких множеств не позволяет в должной мере учитывать различные варианты зависимости между понятиями (объектами), моделируемыми с его помощью, не является достаточно гибким. Так, для описания "общей части" двух нечетких множеств есть лишь две операции - произведение и пересечение. Если применяется первая из них, то фактически предполагается, что множества ведут себя как проекции независимых случайных множеств (см. выше теорему 6). Операция пересечения также накладывает вполне определенные ограничения на вид зависимости между множествами (см. выше теорему 7), причем в этом случае найдены даже необходимые и достаточные условия. Желательно иметь более широкие возможности для моделирования зависимости между множествами (понятиями, объектами). Использование математического аппарата случайных множеств предоставляет такие возможности.

Цель сведения нечетких множеств к случайным состоит в том, чтобы за любой конструкцией из нечетких множеств видеть конструкцию из случайных множеств, определяющую свойства первой, аналогично тому, как плотностью распределения вероятностей мы видим случайную величину. В настоящем пункте приводим результаты по сведению алгебры нечетких множеств к алгебре случайных множеств.

Определение 4. Вероятностное пространство { W , G, P} назовем делимым, если для любого измеримого множества Х G и любого положительного числа , меньшего Р(Х), можно указать измеримое множество такое, что

Пример. Пусть - единичный куб конечномерного линейного пространства, G есть сигма-алгебра борелевских множеств, а P - мера Лебега. Тогда { W , G, P} - делимое вероятностное пространство.

Таким образом, делимое вероятностное пространство - это не экзотика. Обычный куб является примером такого пространства.

Доказательство сформулированного в примере утверждения проводится стандартными математическими приемами, основанными на том, что измеримое множество можно сколь угодно точно приблизить открытыми множествами, последние представляются в виде суммы не более чем счетного числа открытых шаров, а для шаров делимость проверяется непосредственно (от шара Х тело объема отделяется соответствующей плоскостью).

Теорема 8. Пусть даны случайное множество А на делимом вероятностном пространстве { W , G, P} со значениями во множестве всех подмножеств множества У из конечного числа элементов, и нечеткое множество D на У. Тогда существуют случайные множества С 1 , С 2 , С 3 , С 4 на том же вероятностном пространстве такие, что

где B = Proj A.

Доказательство. В силу справедливости законов де Моргана для нечетких (см. теорему 1 выше) и для случайных множеств, а также теоремы 5 выше (об отрицаниях) достаточно доказать существование случайных множеств С 1 и С 2 .

Рассмотрим распределение вероятностей во множестве всех подмножеств множества У , соответствующее случайному множеству С такому, что Proj C = D (оно существует в силу теоремы 3). Построим случайное множество С 2 Исключим элемент только для того же множества У такие, что

и, кроме того, результаты теоретико-множественных операций связаны аналогичными соотношениями

где знак означает, что на рассматриваемом месте стоит символ пересечения случайных множеств, если в определении B m стоит символ пересечения или символ произведения нечетких множеств, и соответственно символ объединения случайных множеств, если в B m стоит символ объединения или символ суммы нечетких множеств.

Ассоциативность

х 1 (х 2 х 3) = (х 1 х 2)х 3 ;

х 1 Ú (х 2 Ú х 3) = (х 1 Ú х 2) Ú х 3 .

Коммутативность

х 1 х 2 = х 2 х 1

х 1 Ú х 2 = х 2 Ú х 1

Дистрибутивность конъюнкции относительно дизъюнкции

х 1 (х 2 Ú х 3) = х 1 х 2 Ú х 1 х 3 .

Дистрибутивность дизъюнкции относительно конъюнкции

х 1 Ú(х 2 × х 3) = (х 1 Úх 2) × (х 1 Úх 3). *

Идемпотентность (тавтология)

Двойное отрицание

Свойства констант

x & 1 = x; (законы универсального множества)

x & 0 = 0; (законы нулевого множества)

Правила (законы) де Моргана

Закон противоречия (дополнительности)

Закон исключения третьего (дополнительности)

Доказательства всех этих формул тривиальны. Один из вариантов –построение таблиц истинности левой и правой частей и их сравнение.

Правила склеивания

Правило склеивания для элементарных конъюнкций следует из распределительного закона, закона дополнительности и закона универсального множества: дизъюнкцию двух соседних конъюнкций можно заменитьодной элементарной конъюнкцией, являющейся общей частьюисходных конъюнкций .

Правило склеивания для элементарных сумм следует из распределительного закона второго рода, закона дополнительности и закона нулевого множества: конъюнкцию двух соседних дизъюнкций можно заменить одной элементарной дизъюнкцией, являющейся общей частьюисходных дизъюнкций .

Правило поглощения

Правило поглощения для суммы двух элементарных произведений следует из распределительного закона первого рода и законов универсального множества: дизъюнкцию двух элементарных конъюнкций, из которых одна является составной частью другой, можно заменить конъюнкцией, имеющейменьшее количество операндов .

Правило поглощения для произведения элементарных сумм следует из распределительного закона второго рода и законов нулевого множества: конъюнкцию двух элементарных дизъюнкций, из которых одна является составной частью другой, можно заменить элементарной дизъюнкцией, имеющей меньшее количество операндов.

Правило развертывания

Это правило определяет действие обратное склеиванию.

Правило развертывания элементарного произведения в логическую сумму элементарных произведений большего ранга (в пределе до r = n, т.е. до конституент единицы, как и будет рассмотрено ниже) следует из законов универсального множества, распределительного закона первого рода и производится в три этапа:

В развертываемое элементарное произведение ранга r вводится в качестве сомножителей n-r единиц, где n- ранг конституенты единицы;

Каждая единица заменяется логической суммой некоторой, не имеющейся в исходном элементарном произведении переменной и ее отрицания: x i v `x i = 1;

Производится раскрытие всех скобок на основе распределительного закона первого рода, что приводит к развертыванию исходного элементарного произведения ранга r в логическую сумму 2 n-r конституент единицы.

Правило развертывания элементарного произведения используется для минимизации функций алгебры логики (ФАЛ).

Правило развертывания элементарной суммы ранга r до произведения элементарных сумм ранга n (конституент нуля) следует их законов нулевого множества (6) и распределительного закона второго рода (14) и производится в три этапа:

В развертываемую сумму ранга r в качестве слагаемых вводится n-r нулей;

Каждый нуль представляется в виде логического произведения некоторой, не имеющейся в исходной сумме переменной и ее отрицания: x i ·`x i = 0;

Получившееся выражение преобразуется на основе распределительного закона второго рода (14) таким образом, чтобы исходная сумма ранга r развернулась в логическое произведение 2 n-r конституент нуля.

16.Понятие полной системы. Примеры полных систем (с доказательством)

Определение. Множество функций алгебры логики A называется полной системой (в P2), если любую функцию алгебры логики можно выразить формулой над A.

Система функций A={ f 1 , f 1 ,…, f m }, являющаяся полной, называется базисом .

Минимальным базисом называется такой базис, для которого удаление хотя бы одной функции f 1 , образующей этот базис, превращает систему функций (f 1 , f 1 ,…, f m) в неполную.

Теорема. Система A = {∨, &, } является полной.

Доказательство. Если функция алгебры логики f отлична от тождественного нуля, то f выражается в виде совершенной дизъюнктивной нормальной формы, в которую входят лишь дизъюнкция, конъюнкция и отрицание. Если же f ≡ 0, то f = x & x . Теорема доказана.

Лемма. Если система A - полная, и любая функция системы A может быть выражена формулой над некоторой другой системой B, то B - также полная система.

Доказательство. Рассмотрим произвольную функцию алгебры логики f (x 1 , …, x n) и две системы функций: A = {g 1 , g 2 , …} и B = {h 1 , h 2 , …}. В силу того, что система A полна, функция f может быть выражена в виде формулы над ней:

f (x 1 , …, x n) = ℑ

где g i = ℜ i

то есть функция f представляется в виде

f (x 1 , …, x n)=ℑ[ℜ1,ℜ2,...]

иначе говоря, может быть представлена формулой над B. Перебирая таким образом все функции алгебры логики, получим, что система B также полна. Лемма доказана.

Теорема. Следующие системы являются полными в P 2:

4) {&, ⊕ , 1}базис Жегалкина.

Доказательство.

1) Известно (теорема 3), что система A = {&, V, } полна. Покажем, что полна система B = { V, . Действительно, из закона де Моргана (x& y) = (x ∨ y) получаем, что x & y = (x ∨ y) , то есть конъюнкция выражается через дизъюнкцию и отрицание, и все функции системы A выражаются формулами над системой B. Согласно лемме система B полна.

2) Аналогично пункту 1: (x ∨ y) = x & y ⇔ x ∨ y =(x & y) и из леммы 2 следует истинность утверждения пункта 2.

3) x | y=(x&y), x | x = x ; x & y = (x | y) = (x | y) | (x | y) и согласно лемме 2 система полна.

4) x = x ⊕1 и согласно лемме 2 система полна.

Теорема доказана.

17.Алгебра Жегалкина. Свойства операций и полнота

Множество булевых функций, заданных в базисе Жегалкина S4={⊕,&,1} называется алгеброй Жегалкина .

Основные свойства.

1. коммутативность

h1⊕h2=h2⊕h1 h1&h2=h2&h1

2. ассоциативность

h1⊕(h2⊕h3)=(h1⊕h2)⊕h3 h1&(h2&h3)=(h1&h2)&h3

3. дистрибутивность

h1&(h2⊕h3)=(h1&h2)⊕(h1&h3)

4. свойства констант

5. h⊕h=0 h&h=h
Утверждение . Через операции алгебры Жегалкина можно выразить все другие булевы функции:

x→y=1⊕x⊕xy

x↓y=1⊕x⊕y⊕xy

18.Полином Жегалкина. Способы построения. Пример.

Полиномом Жегалкина (полиномом по модулю 2) от n переменных x 1 ,x 2 ... x n называется выражение вида:

c 0 ⊕c 1 x 1 ⊕c 2 x 2 ⊕ ... ⊕c n x n ⊕c 12 x 1 x 2 ⊕ ... ⊕c 12 ... n x 1 x 2 ... x n ,

где постоянные C k могут принимать значения 0 ли 1.

Если полином Жегалкина не содержит произведений отдельных переменных, то он называется линейным (линейная функция).

Например, f=x⊕yz⊕xyz и f 1 =1⊕x⊕y⊕z - полиномы, причем вторая является линейной функцией.

Теорема . Каждая булева функция представляется в виде полинома Жегалкина единственным образом.

Приведем основные методы построения полиномов Жегалкина от заданной функции.

1. Метод неопределенных коэффициентов. Пусть P(x 1 ,x 2 ... x n) - искомый полином Жегалкина, реализующий заданную функцию f(x 1 ,x 2 ... x n). Запишем его в виде

P=c 0 ⊕c 1 x 1 ⊕c 2 x 2 ⊕ ... ⊕c n x n ⊕c 12 x 1 x 2 ⊕ ... ⊕c 12 ... n x 1 x 2 ... x n

Найдем коэффициенты C k . Для этого последовательно придадим переменным x 1 ,x 2 ... x n значения из каждой строки таблицы истинности. В итоге получим систему из 2 n уравнений с 2 n неизвестными, имеющую единственное решение. Решив ее, находим коэффициенты полинома P(X 1 ,X 2 ... X n).

2. Метод, основанный на преобразовании формул над множеством связок {,&}. Строят некоторую формулу F над множеством связок {,&}, реализующую данную функцию f(X 1 ,X 2 ... X n). Затем заменяют всюду подформулы вида A на A⊕1, раскрывают скобки, пользуясь дистрибутивным законом (см. свойство 3), а затем применяют свойства 4 и 5.

Пример . Построить полином Жегалкина функции f(X,Y)=X→Y

Решение .
1. (метод неопределенных коэффициентов). Запишем искомый полином в виде:

P=c 0 ⊕c 1 x⊕c 2 y⊕c 12 xy

Пользуясь таблицей истинности импликации получаем, что

f(0,0)=P(0,0)=C 0 =1

f(0,1)=P(0,1)=C 0 ⊕C 2 =1

f(1,0)=P(1,0)=C 0 ⊕C 1 =0

f(1,1)=P(1,1)=C 0 ⊕C 1 ⊕C 2 ⊕C 12 =1

Откуда последовательно находим, C 0 =1, C 1 =1, C 2 =0, C 12 =1

Следовательно: x→y=1⊕X⊕XY.

2. (Метод преобразования формул.). Имеем: x→y=xvy=(xy)=(x(y⊕1)) ⊕1=1⊕x⊕xy
Заметим, что преимущество алгебры Жегалкина (по сравнению с другими алгебрами) состоит в арифметизации логики, что позволяет выполнять преобразования булевых функций довольно просто. Ее недостатком по сравнению с булевой алгеброй является громоздкость формул.

Похожая информация.

Формулы и законы логики

На вводном уроке, посвящённом основам математической логики , мы познакомились с базовыми понятиями этого раздела математики, и сейчас тема получает закономерное продолжение. Помимо нового теоретического, а точнее даже не теоретического – а общеобразовательного материала нас ожидают практические задания, и поэтому если вы зашли на данную страницу с поисковика и/или плохо ориентируетесь в материале, то, пожалуйста, пройдите по вышеуказанной ссылке и начните с предыдущей статьи. Кроме того, для практики нам потребуется 5 таблиц истинности логических операций , которые я настоятельно рекомендую переписать от руки .

НЕ запомнить, НЕ распечатать, а именно ещё раз осмыслить и собственноручно переписать на бумагу – чтобы они были перед глазами:

– таблица НЕ;
– таблица И;
– таблица ИЛИ;
– импликационная таблица;
– таблица эквиваленции.

Это очень важно. В принципе, их было бы удобно занумеровать «Таблица 1», «Таблица 2» и т.д. , но я неоднократно подчёркивал изъян такого подхода – как говорится, в одном источнике таблица окажется первой, а в другом – сто первой. Поэтому будем использовать «натуральные» названия. Продолжаем:

На самом деле с понятием логической формулы вы уже знакомы. Приведу стандартное, но довольно-таки остроумное определение : формулами алгебры высказываний называются:

1) любые элементарные (простые) высказывания ;

2) если и – формулы, то формулами также являются выражения вида
.

Никаких других формул нет.

В частности формулой является любая логическая операция, например логическое умножение . Обратите внимание на второй пункт – он позволяет рекурсивным образом «создать» сколь угодно длинную формулу. Поскольку – формулы, то – тоже формула; так как и – формулы, то – тоже формула и т.д. Любое элементарное высказывание (опять же согласно определению) может входить в формулу неоднократно.

Формулой не является, например, запись – и здесь прослеживается очевидная аналогия с «алгебраическим мусором» , из которого не понятно – нужно ли числа складывать или умножать.

Логическую формулу можно рассматривать, как логическую функцию . Запишем в функциональном виде ту же конъюнкцию:

Элементарные высказывания и в этом случае играют роль аргументов (независимых переменных), которые в классической логике могут принимать 2 значения: истина или ложь . Далее для удобства я буду иногда называть простые высказывания переменными .

Таблица, описывающая логическую формулу (функцию) называется, как уже было озвучено, таблицей истинности . Пожалуйста – знакомая картинка:

Принцип формирования таблицы истинности таков: «на входе» нужно перечислить все возможные комбинации истины и лжи, которые могут принимать элементарные высказывания (аргументы). В данном случае в формулу входят два высказывания, и нетрудно выяснить, что таких комбинаций четыре. «На выходе» же получаем соответствующие логические значения всей формулы (функции).

Надо сказать, что «выход» здесь получился «в один шаг», но в общем случае логическая формула является более сложной. И в таких «непростых случаях» нужно соблюдать порядок выполнения логических операций :

– в первую очередь выполняется отрицание ;
– во вторую очередь – конъюнкция ;
– затем – дизъюнкция ;
– потом импликация ;
– и, наконец, низший приоритет имеет эквиваленция .

Так, например, запись подразумевает, что сначала нужно осуществить логическое умножение , а затем – логическое сложение: . Прямо как в «обычной» алгебре – «сначала умножаем, а затем складываем».

Порядок действий можно изменить привычным способом – скобками:
– здесь в первую очередь выполняется дизъюнкция и только потом более «сильная» операция.

Наверное, все понимают, но на всякий пожарный : и – это две разные формулы! (как в формальном, так и в содержательном плане)

Составим таблицу истинности для формулы . В данную формулу входят два элементарных высказывания и «на входе» нам нужно перечислить все возможные комбинации единиц и нулей. Чтобы избежать путаницы и разночтений договоримся перечислять комбинации строго в таком порядке (который я, собственно, де-факто использую с самого начала) :

В формулу входят две логические операции, и согласно их приоритету, в первую очередь нужно выполнить отрицание высказывания . Ну что же, отрицаем столбец «пэ» – единицы превращаем в нули, а нули – в единицы:

На втором шаге смотрим на столбцы и и применяем к ним операцию ИЛИ . Немного забегая вперёд, скажу, что дизъюнкция перестановочна ( и – это одно и то же) , и поэтому столбцы можно анализировать в привычном порядке – слева направо. При выполнении логического сложения удобно использовать следующее прикладное рассуждение: «Если два нуля – ставим ноль, если хотя бы одна единица – единицу» :

Таблица истинности построена. А теперь вспомним старую-добрую импликацию:

…внимательно-внимательно… смотрим на итоговые колонки…. В алгебре высказываний такие формулы называются равносильными или тождественными :

(три горизонтальные чёрточки – это значок тождества)

В 1-й части урока я обещал выразить импликацию через базовые логические операции, и выполнение обещания не заставило себя ждать! Желающие могут вложить в импликацию содержательный смысл (например, «Если идёт дождь, то на улице сыро») и самостоятельно проанализировать равносильное утверждение .

Сформулируем общее определение : две формулы называются равносильными (тождественными) , если они принимают одинаковые значения при любом наборе значений, входящих в эти формулы переменных (элементарных высказываний) . Также говорят, что «формулы равносильны, если совпадают их таблицы истинности» , но мне не очень нравится эта фраза.

Задание 1

Составить таблицу истинности для формулы и убедиться в справедливости знакомого вам тождества .

Ещё раз повторим порядок решения задачи:

1) Так как в формулу входят две переменные, то всего будет 4 возможных набора нулей и единиц. Записываем их в оговорённом выше порядке.

2) Импликации «слабее» конъюнкции, но они располагаются в скобках. Заполняем столбец , при этом удобно использовать следующее прикладное рассуждение: «если из единицы следует ноль, то ставим ноль, во всех других случаях – единицу» . Далее заполняем столбец для импликации , и при этом, внимание! – столбцы и следует анализировать «справа налево»!

3) И на завершающем этапе заполняем итоговый столбец . А здесь удобно рассуждать так: «если в столбцах и две единицы, то ставим единицу, во всех остальных случаях – ноль» .

И, наконец, сверяемся с таблицей истинности эквиваленции .

Основные равносильности алгебры высказываний

С двумя из них мы только что познакомились, но ими дело, понятно, не огранивается. Тождеств довольно много и я перечислю самые важные и самые известные из них:

Коммутативность конъюнкции и коммутативность дизъюнкции

Коммутативность – это перестановочность:

Знакомые с 1-го класса правила: «От перестановки множителей (слагаемых) произведение (сумма) не меняется» . Но при всей кажущейся элементарности этого свойства, справедливо оно далеко не всегда, в частности, некоммутативным является умножение матриц (в общем случае их переставлять нельзя) , а векторное произведение векторов – антикоммутативно (перестановка векторов влечёт за собой смену знака) .

И, кроме того, здесь я снова хочу подчеркнуть формализм математической логики. Так, например, фразы «Студент сдал экзамен и выпил» и «Студент выпил и сдал экзамен» различны с содержательной точки зрения, но неразличимы с позиций формальной истинности. …Таких студентов знает каждый из нас, и из этических соображений мы не будет озвучивать конкретных имён =)

Ассоциативность логического умножения и сложения

Или, если «по-школьному» – сочетательное свойство:

Дистрибутивные свойства

Обратите внимание, что во 2-м случае будет некорректно говорить о «раскрытии скобок», в известном смысле здесь «фикция» – ведь их можно убрать вообще: , т.к. умножение – это более сильная операция.

И опять же – эти, казалось бы, «банальные» свойства выполняются далеко не во всех алгебраических системах, и, более того, требуют доказательства (о которых мы очень скоро поговорим) . К слову, второй дистрибутивный закон несправедлив даже в нашей «обычной» алгебре. И в самом деле:

Закон идемпотентности

Что делать, латынь....

Прямо какой-то принцип здоровой психики: «я и я – это я», «я или я – это тоже я» =)

И тут же несколько похожих тождеств:

…мда, что-то я даже подзавис… так и доктором философии завтра можно проснуться =)

Закон двойного отрицания

Ну а здесь уже напрашивается пример с русским языком – все прекрасно знают, что две частицы «не» означают «да». А для того, чтобы усилить эмоциональную окраску отрицания нередко используют три «не»:
– даже с крохотным доказательством получилось!

Законы поглощения

– «а был ли мальчик?» =)

В правом тождестве скобки можно опустить.

Законы де Моргана

Предположим, что строгий Преподаватель (имя которого вам тоже известно:)) ставит экзамен, если – Студент ответил на 1-й вопрос и – Студент ответил на 2-й вопрос . Тогда высказывание , гласящее о том, что Студент не сдал экзамен , будет равносильно утверждению – Студент не ответил на 1-й вопрос или на 2-й вопрос .

Как уже отмечалось выше, равносильности подлежат доказательству, которое стандартно осуществляется с помощью таблиц истинности. В действительности мы уже доказали равносильности, выражающие импликацию и эквиваленцию, и сейчас настало время закрепить технику решения данной задачи.

Докажем тождество . Поскольку в него входит единственное высказывание , то «на входе» возможно всего лишь два варианта: единица либо ноль. Далее приписываем единичный столбец и применяем к ним правило И :

В результате «на выходе» получена формула, истинность которой совпадает с истинностью высказывания . Равносильность доказана.

Да, это доказательство является примитивным (а кто-то скажет, что и «тупым») , но типичный Преподаватель по матлогике вытрясет за него душу. Поэтому даже к таким простым вещам не стОит относиться пренебрежительно.

Теперь убедимся, например, в справедливости закона де Моргана .

Сначала составим таблицу истинности для левой части. Поскольку дизъюнкция находится в скобках, то в первую очередь выполняем именно её, после чего отрицаем столбец :

Далее составим таблицу истинности для правой части . Здесь тоже всё прозрачно – в первую очередь проводим более «сильные» отрицания, затем применяем к столбцам правило И :

Результаты совпали, таким образом, тождество доказано.

Любую равносильность можно представить в виде тождественно истинной формулы . Это значит, что ПРИ ЛЮБОМ исходном наборе нулей и единиц «на выходе» получается строго единица. И этому есть очень простое объяснение: так как таблицы истинности и совпадают, то, разумеется, они эквивалентны.Соединим, например, эквиваленцией левую и правую часть только что доказанного тождества де Моргана:

Или, если компактнее:

Задание 2

Доказать следующие равносильности:

б)

Краткое решение в конце урока. Не ленимся! Постарайтесь не просто составить таблицы истинности, но ещё и чётко сформулировать выводы. Как я недавно отмечал, пренебрежение простыми вещами может обойтись очень и очень дорого!

Продолжаем знакомиться с законами логики!

Да, совершенно верно – мы с ними уже вовсю работаем:

Истина при , называется тождественно истинной формулой или законом логики .

В силу обоснованного ранее перехода от равносильности к тождественно истинной формуле , все перечисленные выше тождества представляют собой законы логики.

Формула, которая принимает значение Ложь при любом наборе значений входящих в неё переменных , называется тождественно ложной формулой или противоречием .

Фирменный пример противоречия от древних греков:
– никакое высказывание не может быть истинным и ложным одновременно.

Доказательство тривиально:

«На выходе» получены исключительно нули, следовательно, формула действительно тождественна ложна .

Однако и любое противоречие – это тоже закон логики, в частности:

Нельзя объять столь обширную тему в одной-единственной статье, и поэтому я ограничусь ещё лишь несколькими законами:

Закон исключённого третьего

– в классической логике любое высказывание истинно или ложно и третьего не дано. «Быть или не быть» – вот в чём вопрос.

Самостоятельно составьте табличку истинности и убедитесь в том, что это тождественно истинная формула.

Закон контрапозиции

Этот закон активно муссировался, когда мы обсуждали суть необходимого условия , вспоминаем: «Если во время дождя на улице сыро, то из этого следует, что если на улице сухо, то дождя точно не было» .

Также из данного закона следует, что если справедливой является прямая теорема , то обязательно истинным будет и утверждение , которое иногда называют противоположной теоремой.

Если истинна обратная теорема , то в силу закона контрапозиции , справедлива и теорема, противоположная обратной :

И снова вернёмся к нашим содержательным примерам: для высказываний – число делится на 4, – число делится на 2 справедливы прямая и противоположная теоремы, но ложны обратная и противоположная обратной теоремы. Для «взрослой» же формулировки теоремы Пифагора истинны все 4 «направления».

Закон силлогизма

Тоже классика жанра: «Все дубы – деревья, все деревья – растения, следовательно, все дубы – растения» .

Ну и здесь опять хочется отметить формализм математической логики: если наш строгий Преподаватель думает, что некий Студент – есть дуб, то с формальной точки зрения данный Студент, безусловно, растение =) …хотя, если задуматься, то может быть и с неформальной тоже =)

Составим таблицу истинности для формулы . В соответствии с приоритетом логических операций, придерживаемся следующего алгоритма:

1) выполняем импликации и . Вообще говоря, можно сразу выполнить и 3-ю импликацию, но с ней удобнее (и допустимо!) разобраться чуть позже;

2) к столбцам применяем правило И ;

3) вот теперь выполняем ;

4) и на завершающем шаге применяем импликацию к столбцам и .

Не стесняйтесь контролировать процесс указательным и средним пальцем:))

Из последнего столбца, думаю, всё понятно без комментариев:
, что и требовалось доказать.

Задание 3

Выяснить, будет ли являться законом логики следующая формула:

Краткое решение в конце урока. Да, и чуть не забыл – давайте условимся перечислять исходные наборы нулей и единиц в точно таком же порядке, что и при доказательстве закона силлогизма. Строки конечно, можно и переставить, но это сильно затруднит сверку с моим решением.

Преобразование логических формул

Помимо своего «логического» назначения, равносильности широко используются для преобразования и упрощения формул. Грубо говоря, одну часть тождества можно менять на другую. Так, например, если в логической формуле вам встретился фрагмент , то по закону идемпотентности вместо него можно (и нужно) записать просто . Если вы видите , то по закону поглощения упрощайте запись до . И так далее.

Кроме того, есть ещё одна важная вещь: тождества справедливы не только для элементарных высказываний, но и для произвольных формул. Так, например:

, где – любые (сколь угодно сложные) формулы.

Преобразуем, например, сложную импликацию (1-е тождество) :

Далее применим к скобке «сложный» закон де Моргана, при этом, в силу приоритета операций, именно закон , где :

Скобки можно убрать, т.к. внутри находится более «сильная» конъюнкция:

Ну, а с коммутативностью вообще всё просто – даже обозначать ничего не нужно… что-то запал мне в душу закон силлогизма:))

Таким образом, закон можно переписать и в более затейливом виде:

Проговорите вслух логическую цепочку «с дубом, деревом, растением», и вы поймёте, что от перестановки импликаций содержательный смысл закона нисколько не изменился. Разве что формулировка стала оригинальнее.

В качестве тренировки упросим формулу .

С чего начать? Прежде всего, разобраться с порядком действий: здесь отрицание применено к целой скобке, которая «скреплена» с высказыванием «чуть более слабой» конъюнкцией. По существу, перед нами логическое произведение двух множителей: . Из двух оставшихся операций низшим приоритетом обладает импликация, и поэтому вся формула имеет следующую структуру: .

Как правило, на первом шаге (шагах) избавляются от эквиваленции и импликации (если они есть) и сводят формулу к трём основным логическим операциям. Что тут скажешь…. Логично.

(1) Используем тождество . А нашем случае .

Затем обычно следуют «разборки» со скобками. Сначала всё решение, затем комментарии. Чтобы не получилось «масло масляное», буду использовать значки «обычного» равенства: